思路分析:将直线方程与圆锥曲线方程联立,消去y,令Δ>0,利用韦达定理来求解.
解:当曲线y=x2+px+1与直线y=2x有两个交点时,
由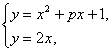
知x2+(p-2)x+1=0应有两个不同的实数根.又Δ=(p-2)2-4>0时,p<0或p>4,
∴当p<0或p>4时,x1+x2=2-p,x1·x2=1.
因此,u=(1+px1+x12)(1+px2+x22)=(x1x2)2+x12+x22+1+(x1+x2)(1+x1x2)p+x1x2p2=2+(x1+x2)2-2x1x2+
2(2-p)p+p2=(2-p)2+2(2-p)p+p2=4(定值).
故u的值与p无关.