已知a、b为正整数,设两直线l1:y=bx与l2:y=x的交点为P1(x1,y1),且对于n≥2
已知a、b为正整数,设两直线l
1:y=b
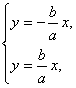
x与l
2:y=

x的交点为P
1(x
1,y
1),且对于n≥2的自然数,两点(0,b),(x
n-1,0)的连线与直线y=
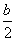
x交于点P
n(x
n,y
n).
(1)求P1、P2的坐标.
(2)猜想Pn的坐标公式.
解析:两直线的交点坐标可通过解方程组解出,由两点坐标又可写出新的直线方程,从而猜出P
n的坐标.
解
:(1)解方程组
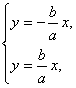
得P
1(

,
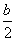
).过(0,b),(
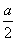
,0)两点的直线方程为
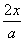
+
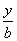
=1,与y=
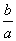
x联立解得P
2(
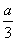
,
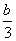
).(2)由(1)可猜想P
n(

,

).
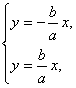 得P1(
得P1(