已知函数f（x）=ax2﹣4ln（x﹣1）． （Ⅰ）当a=1时，求f（x）的单调区

已知函数f（x）=ax²﹣4ln（x﹣1）．

（Ⅰ）当a=1时，求f（x）的单调区间；

（Ⅱ）若对一切x∈[2，e+1]，f（x）≤4恒成立，求实数a的取值范围．

考点： 利用导数求闭区间上函数的最值；利用导数研究函数的单调性．

专题： 导数的综合应用．

分析： （I）当a=1时，f（x）=x²﹣4ln（x﹣1）（x＞1），f′（x）=，分别解出f′（x）＞0，f′（x）＜0，即可得出单调区间；

（II）对一切x∈[2，e+1]，f（x）≤4恒成立⇔a≤，x∈[2，e+1]．令u（x）=，x∈[2，e+1]，利用导数研究其单调性极值与最值，即可得出．

解答： 解：（I）当a=1时，f（x）=x²﹣4ln（x﹣1）（x＞1），f′（x）=2x﹣=，

当x＞2时，f′（x）＞0，此时函数f（x）单调递增；当1＜x＜2时，f′（x）＜0，此时函数f（x）单调递减．

∴函数f（x）单调递增区间是（2，+∞）；函数f（x）单调递减区间是（1，2）．

（II）对一切x∈[2，e+1]，f（x）≤4恒成立⇔a≤，x∈[2，e+1]．

令u（x）=，x∈[2，e+1]，

u′（x）==，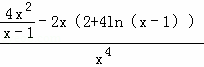

令v（x）=4x﹣8﹣8ln（x﹣1），x∈[2，e+1]，

v′（x）=4﹣=，

当x∈[2，3）时，v′（x）＜0，此时函数v（x）单调递减；当x∈（3，e+1]时，v′（x）＞0，此时函数v（x）单调递增．

而v（2）=0，v（e+1）=4（e+1）﹣8﹣8=4（e﹣3）＜0，

∴u′（x）≤0（只有x=2时取等号），

∴函数u（x）单调递减，

∴当x=e+1时，函数u（x）取得极小值即最小值，u（e+1）=．

∴a，即为a的取值范围．