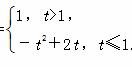已知二次函数f(x)＝ax2＋bx(a，b为常数，且a≠0)满足条件：f(x－1)＝f(3－x)，且方程f(x)＝2x有两等根.
(1)求f(x)的解析式；
(2)求f(x)在[0，t]上的最大值.
已知二次函数f(x)＝ax2＋bx(a，b为常数，且a≠0)满足条件：f(x－1)＝f(3－x)，且方程f(x)＝2x有两等根.
(1)求f(x)的解析式；
(2)求f(x)在[0，t]上的最大值.
解 (1)因为方程f(x)＝2x有两等根，即方程ax2＋(b－2)x＝0有两等根，所以Δ＝(b－2)2＝0，得b＝2，因为f(x－1)＝f(3－x)，得
＝1，所以x＝1是函数图象的对称轴，所以－
＝1，所以a＝－1，所以f(x)＝－x2＋2x.
(2)因为函数f(x)＝－x2＋2x的图象对称轴为x＝1，x∈[0，t]，所以当t≤1时，f(x)在[0，t]上是增函数，所以f(x)的最大值为f(t)＝－t2＋2t.
当t>1时f(x)在[0，1]上是增函数，在[1，t]上是减函数，所以f(x)的最大值为f(1)＝1.
综上知f(x)的最大值为f(x)max＝