пјҲ1пјүз”Ёж•°еӯҰеҪ’зәіжі•иҜҒжҳҺ:bnвүӨ![]() ;
;
пјҲ2пјүиҜҒжҳҺ:Snпјң![]() .
.
пјҲ1пјүз”Ёж•°еӯҰеҪ’зәіжі•иҜҒжҳҺ:bnвүӨ![]() ;
;
пјҲ2пјүиҜҒжҳҺ:Snпјң![]() .
.
иҜҒжҳҺпјҡ(1)еҪ“xвүҘ0ж—¶,f(x)=1+![]() вүҘ1.еӣ дёәa1=1пјҢжүҖд»ҘanвүҘ1(nвҲҲN
вүҘ1.еӣ дёәa1=1пјҢжүҖд»ҘanвүҘ1(nвҲҲN
дёӢйқўз”Ёж•°еӯҰеҪ’зәіжі•иҜҒжҳҺдёҚзӯүејҸbnвүӨ![]() .
.
пјҲв… пјүеҪ“n=1ж—¶пјҢb1=![]() -1пјҢдёҚзӯүејҸжҲҗз«ӢпјҢ
-1пјҢдёҚзӯүејҸжҲҗз«ӢпјҢ
пјҲв…ЎпјүеҒҮи®ҫеҪ“n=kж—¶пјҢдёҚзӯүејҸжҲҗз«ӢпјҢеҚіbkвүӨ![]() .
.
йӮЈд№Ҳbk+1=|ak+1-![]() |=
|=![]() .
.
жүҖд»ҘпјҢеҪ“n=k+1ж—¶пјҢдёҚзӯүејҸд№ҹжҲҗз«Ӣ.
ж №жҚ®пјҲв… пјүе’ҢпјҲв…ЎпјүпјҢеҸҜзҹҘдёҚзӯүејҸеҜ№д»»ж„ҸnвҲҲN
*йғҪжҲҗз«Ӣ.пјҲ2пјүз”ұпјҲв… пјүзҹҘпјҢbnвүӨ![]() .жүҖд»Ҙ
.жүҖд»Ҙ
Sn=b1+b2+вҖҰ+bnвүӨ(![]() -1)+
-1)+![]()
=пјҲ![]() -1пјүВ·
-1пјүВ·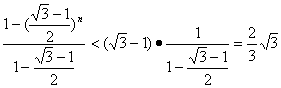 .
.
ж•…еҜ№д»»ж„ҸnвҲҲN
*,Snпјң