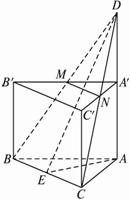
解析：取BC的中点E，分别连结DE和AE，则AE⊥BC，DE⊥BC，
∴∠DEA为截面与底面所成的二面角，即∠DEA=60°.
∵AE=
×4=
cm,
∴AD=AE·tan60°=6 cm ,AD＞AA′.
∴截面不与棱AA′相交而与平面A′B′C′相交于MN.
由面面平行的性质定理知MN∥BC，截面是一个等腰梯形MNCB，
如图，A′D=2 cm,∵DE=2AE=
cm ,
∴S△BCD =
BC×DE=
cm2.
∵MN∥BC,
∴
.
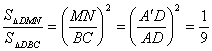∴S△MND=
m2.
∴截面梯形的面积为S△BCD-S△MND=
cm2.