如图，已知四棱锥P﹣ABCD的底面为矩形，PA⊥底面ABCD，且PA=AD=1，AB=
，点E，F分别为AB、PC中点．
（1）求证：EF⊥PD；
（2）求点E到平面PDC的距离．
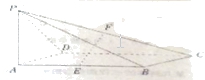
如图，已知四棱锥P﹣ABCD的底面为矩形，PA⊥底面ABCD，且PA=AD=1，AB=，点E，F分别为AB、PC中点．
（1）求证：EF⊥PD；
（2）求点E到平面PDC的距离．
【考点】点、线、面间的距离计算；空间中直线与直线之间的位置关系．
【专题】数形结合；综合法；空间位置关系与距离．
【分析】（1）取PD的中点M，可得AEFM为平行四边形，AM∥EF，根据AM⊥PD，证得EF⊥PD．
（2）设点E到平面PDC的距离为h，由于AE平行于平面PCD，故点E到平面PDC的距离等于点A到平面PDC的距离，再根据由VP﹣ACD=VE﹣PCD，求得h的值．
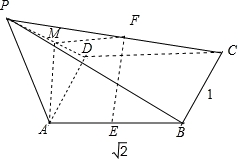
【解答】解：（1）如图所示：已知四棱锥P﹣ABCD的底面为矩形，PA⊥底面ABCD，取PD的中点M，
∵E为AB的中点，
故AE∥MF，AE=MF，∴AEFM为平行四边形，∴AM∥EF．
由PA=AD=1，AB=
，可得PAD为等腰直角三角形，AM⊥PD，故EF⊥PD．
（2）由于PCD PCE都是直角三角形，利用勾股定理求得PC=2，PD=，
设点E到平面PDC的距离为h．
由于AE平行于平面PCD，故点E到平面PDC的距离等于点A到平面PDC的距离．
由VP﹣ACD=VE﹣PCD 可得 
•S△ACD•PA=•S△PCD•h，
可得•S△ACD•PA=S△PCD•h，即
•AD•CD•PA=•PD•CD•h，即AD•PA=PD•h，
即1×1=
•h，求得 h=
点E到平面PDC的距离为．
【点评】本题主要考查证明直线和直线垂直的方法，用等体积法求点到平面的距离，体现了转化、数形结合的数学思想，属于中档题．