若函数
对任意的
，均有
，则称函数具有性质
.
（Ⅰ）判断下面两个函数是否具有性质，并说明理由.
①
； ②
.
（Ⅱ）若函数具有性质，且
（
），
求证：对任意
有
；
（Ⅲ）在（Ⅱ）的条件下，是否对任意
均有
.若成立给出证明，若不成立给出反例.
若函数对任意的，均有，则称函数具有性质.
（Ⅰ）判断下面两个函数是否具有性质，并说明理由.
①； ②.
（Ⅱ）若函数具有性质，且（），
求证：对任意有；
（Ⅲ）在（Ⅱ）的条件下，是否对任意均有.若成立给出证明，若不成立给出反例.
（Ⅰ）证明：①函数
具有性质.
，
即，
此函数为具有性质.
②函数
不具有性质.
例如，当
时，
，
，
所以，
此函数不具有性质.
（Ⅱ）假设
为
中第一个大于
的值，
则
，
因为函数具有性质，
所以，对于任意，均有
，
所以
，
所以
，
与
矛盾，
所以，对任意的有
.
（Ⅲ）不成立.
例如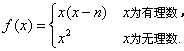
证明：当
为有理数时，
均为有理数，
，
当为无理数时，均为无理数，
所以，函数对任意的，均有，
即函数具有性质.
而当
（
）且当为无理数时，
.
所以，在（Ⅱ）的条件下，“对任意均有”不成立
（其他反例仿此给分，
如
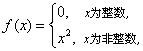等.）