(1)жұӮf(x)зҡ„и§ЈжһҗиЎЁиҫҫејҸпјӣ
(2)иҜҒжҳҺеҪ“nвҲҲN*ж—¶пјҢжңүbnвүӨ(![]() )nпјҺ
)nпјҺ
(1)жұӮf(x)зҡ„и§ЈжһҗиЎЁиҫҫејҸпјӣ
(2)иҜҒжҳҺеҪ“nвҲҲN*ж—¶пјҢжңүbnвүӨ(![]() )nпјҺ
)nпјҺ
(1)и§Јпјҡз”ұf(x)жҳҜеҘҮеҮҪж•°пјҢеҫ— b=c=0.В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
з”ұ|f(x)|min=2![]() пјҢеҫ—a=2пјҢж•…f(x)=
пјҢеҫ—a=2пјҢж•…f(x)=![]() .В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
.В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
(2)иҜҒжҳҺпјҡan+1=![]() =
=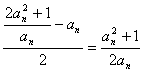 пјҢ
пјҢ
bn+1=![]() =
=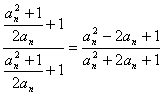 =(
=(![]() )2=
)2=![]() .В В В В В В В В В В В В В В В В В
.В В В В В В В В В В В В В В В В В
вҲҙbn=bn-12=bn-24=вҖҰ=![]() пјҢиҖҢb1=
пјҢиҖҢb1=![]() ,
,
вҲҙbn=![]() .В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
.В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
еҪ“n=1ж—¶пјҢb1=![]() пјҢе‘ҪйўҳжҲҗз«Ӣ.В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҢе‘ҪйўҳжҲҗз«Ӣ.В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
еҪ“nвүҘ2ж—¶,вҲө2nпјҚ1пјқпјҲ1пјӢ1пјүnпјҚ1пјқ1пјӢ![]() +
+![]() +вҖҰ+
+вҖҰ+![]() вүҘ1+
вүҘ1+![]() =n,
=n,
вҲҙ![]() пјң(
пјң(![]() )nпјҢеҚіbnвүӨ(
)nпјҢеҚіbnвүӨ(![]() )nпјҺ
)nпјҺ