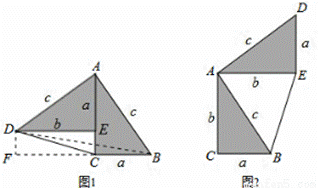
勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感。他惊喜地发现：当两个全等的直
角三角形如图1或图2摆放时，都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：.
证明：连结DB，过点D作BC边上的高DF，则DF=EC= b - a，
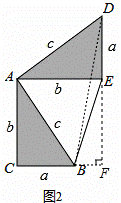
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°.
求证：.
证明：
勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感。他惊喜地发现：当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：.
证明：连结DB，过点D作BC边上的高DF，则DF=EC= b - a，
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°.
求证：.
证明：
证明：连结BD，过点B作DE边上的高BF，则BF=b-a，
∵
又∵，
∴=
∴．
