(满分12分)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,
(满分12分)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.

(1)求证:∠ADB=∠E;
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由.
(3)当AB=5,BC=6时,求⊙O的半径.
(1)略
(2)是
(3)

解析:
(1)在△ABC中,∵AB=AC,∴∠ABC=∠C.
∵DE∥BC,∴∠ABC=∠E,
∴∠E=∠C.
又∵∠ADB=∠C, ∴∠ADB=∠E.
(2)当点D是弧BC的中点时,DE是⊙O的切线.
理由是:当点D是弧BC的中点时,则有AD⊥BC,且AD过圆心O.
又∵DE∥BC,∴ AD⊥ED.
∴ DE是⊙O的切线.
(3)连结BO、AO,并延长AO交BC于点F, 则AF⊥BC,且BF=
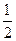
BC=3.
又∵AB=5,∴AF=4.
设⊙O的半径为
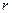
,
在Rt△OBF中,OF=4-
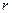
,OB=
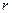
,BF=3,
∴
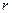

=3
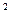
+(4-
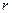
)

解得
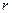
=

,
∴⊙O的半径是



 解析:
解析: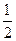 BC=3.
BC=3.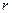 ,
,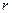 ,OB=
,OB=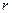 ,BF=3,
,BF=3, 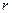
 =3
=3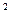 +(4-
+(4-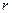 )
)
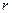 =
= ,
, 