 ∥
∥ ,
, ,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为
,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为 。
。
【小题1】求CD的长;
【小题2】当四边形PBQD为平行四边形时,求四边形PBQD的周长;
【小题3】在点P、点Q的运动过程中,是否存在某一时刻,使得
 的面积为20
的面积为20 ,若存在,请求出所有满足条件的
,若存在,请求出所有满足条件的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。  ∥
∥ ,
, ,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为
,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为 。
。
 的面积为20
的面积为20 ,若存在,请求出所有满足条件的
,若存在,请求出所有满足条件的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。  =
=
 ,
, .解析:
.解析:

 ,解得
,解得 2分
2分

 =
= 2分
2分 时,如图
时,如图

 1分
1分 时,如图
时,如图
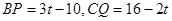

 △=-44〈0,所以方程无实数解 1分
△=-44〈0,所以方程无实数解 1分
 ,则有PQ=
,则有PQ=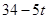
 ,
, 〈6,舍去
〈6,舍去  ,则有PQ=
,则有PQ=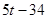
 ,
, 3分
3分 ,
, .
.