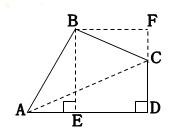
如图，四边形ABCD中，∠ABC＝90°，CD⊥AD，
，
（1）求证：AB=BC；
（2）过点B作BE⊥AD于E，若四边形ABCD的面积为
，求BE的长．
如图，四边形ABCD中，∠ABC＝90°，CD⊥AD，，
（1）求证：AB=BC；
（2）过点B作BE⊥AD于E，若四边形ABCD的面积为，求BE的长．
（1）连接AC
，由勾股定理得
，
，又，所以
，所以
，所以AB=BC．
（2）
．
【解析】
试题分析：（1）连接AC，由勾股定理得，又，所以，所以，问题得证；
（2）过点B作BF⊥BE，延长DC交BF于F，即可证得△ABE≌△CBF，则S四边形BEDF=S四边形ABCD＝，又四边形BEDF为正方形，则BE＝．
试题解析：（1）连接AC，由勾股定理得，，又，所以，所以，所以AB=BC．
（2）过点B作BF⊥BE，延长DC交BF于F，因为∠AEB=∠F，∠ABE=∠CBF，AB=BC，所以△ABE≌△CBF，所以BF=BE, 四边形BEDF为正方形,则S四边形BEDF=S四边形ABCD＝，又四边形BEDF为正方形，所以BE＝．
【难度】一般