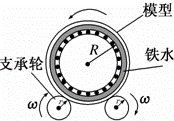
如图所示,在竖直放置的离心浇铸装置中,电动机带动两个支承轮同向转动,管状模型放在这两个支承轮上靠摩擦带动,支承轮与管状模型间不打滑.铁水注入之后,由于离心作用,铁水紧紧靠在模型的内壁上,从而可得到密实的铸件,浇铸时支承轮转速不能过低,否则,铁水会脱离模型内壁,产生次品.已知管状模型内壁半径为R,支承轮的半径为r,重力加速度为g,则支承轮转动的最小角速度ω为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
如图所示,在竖直放置的离心浇铸装置中,电动机带动两个支承轮同向转动,管状模型放在这两个支承轮上靠摩擦带动,支承轮与管状模型间不打滑.铁水注入之后,由于离心作用,铁水紧紧靠在模型的内壁上,从而可得到密实的铸件,浇铸时支承轮转速不能过低,否则,铁水会脱离模型内壁,产生次品.已知管状模型内壁半径为R,支承轮的半径为r,重力加速度为g,则支承轮转动的最小角速度ω为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
考点:线速度、角速度和周期、转速.
专题:匀速圆周运动专题.
分析:经过最高点的铁水要紧压模型内壁,否则,铁水会脱离模型内壁,故临界情况是重力恰好提供向心力,根据牛顿第二定律列式求解管状模型转动的线速度;然后结合v=rω求解支承轮转动的最小角速度.
解答: 解:经过最高点的铁水要紧压模型内壁,临界情况是重力恰好提供向心力,根据牛顿第二定律,有:
mg=m![]()
解得:
v=![]()
支承轮与模型是同缘传动,边缘点线速度相等,故支承轮边缘点的线速度也为![]() ;
;
故支承轮转动的最小角速度ω为:![]()
故选:B.
点评:本题关键是明确铁水恰后不脱离模型内壁的临界情况时重力恰好提供向心力,然后结合牛顿第二定律和v=rω列式求解,不难.