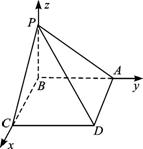
首页 / 四棱锥P—ABCD的底面是边长为a的正方形，PB⊥面ABCD，证明无论四棱锥

四棱锥P—ABCD的底面是边长为a的正方形，PB⊥面ABCD，证明无论四棱锥

四棱锥P—ABCD的底面是边长为a的正方形，PB⊥面ABCD，证明无论四棱锥的高怎样变化，面PAD与面PCD所成的二面角恒大于90°.

答案

证明：以B为坐标原点，BC、BA、BP分别为x轴，y轴,z轴建立空间直角坐标系，设P（0，0，b）,因为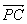=（a,0,-b）, =(a,a,-b)，设n

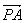
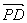
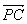
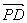
1=(x,y,z) 是平面PAD的一个法向量，则n1·=ay-bz=0,n1·=ax+ay-bz=0,令z=a得n1=(0,b,a).设n2=(x1,y1,z1)是平面PCD的一个法向量，则n2·=ax1-bz1=0,n2·=ax1+ay1-bz1=0,解之得n2=(-b,0,-a),而n1·n2=-a2＜0,所以，cosθ＜0，即无论四棱锥的高怎样变化,平面PAD与平面PCD所成的二面角θ恒大于90°.

 

相关题目

下列现实生活中的场景涉及到的科技发明，属于第三次科技
下列现实生活中的场景涉及到的科技发明，属于第三次科技革命的是 A．坐飞机去开会                         B．上网发电子邮件 C．乘公共
某文章认为：盲目输入西方学说，导致国家基本政治道德原
某文章认为：盲目输入西方学说，导致国家基本政治道德原则丧失、精神破产，造成通俗主义、平凡主义受推崇，盲从欧美之风盛行。该文章针对的是(
某同学用如图所示的实验装置探究阻力对小车运动的影响。
某同学用如图所示的实验装置探究阻力对小车运动的影响。他在水平桌面上分别铺上毛巾、棉布、木板，让小车从斜面上的同一位置由静止滑下，在小
已知456456=23´a´7´11´13´b，其中a、b均为质数。若b>a，则b-a
已知456456=23´a´7´11´13´b，其中a、b均为质数。若b>a，则b-a之值为何？A．12B．14C．16 D．18
100ml 6mol/L H2SO4与过量锌粉反应，一定温度下，为了减缓反应
100ml 6mol/L H2SO4与过量锌粉反应，一定温度下，为了减缓反应进行的速率，但又不影响生成氢气的总量，可向反应物中加入适量的（   ）          
------_________________? ------ He is handsome, kind and honest. A．What is Tom
------_________________? ------ He is handsome, kind and honest. A．What is Tom?                                    B．What does Tom look like?    C．What is T
“感动中国2008年度人物”评选结果揭晓，获得“2008年感动中
“感动中国2008年度人物”评选结果揭晓，获得“2008年感动中国特别奖”的是 A．张艺谋奥运团队                                    
已知二次函数y=ax2+bx的图象经过点A（-1，1），则ab有  (   )
已知二次函数y=ax2+bx的图象经过点A（-1，1），则ab有  (   ) A．最小值0;B．最大值 1;C．最大值2;D．有最小值

最新题目

对下列句中加点词的解释不正确的一项是 A.长不满七尺，滑
在直角坐标系中，已知△ABC三个顶点的坐标分别是 A（0，）
把方程化成的形式，则m、n的值是（        ） A、4，13 
2010年6月11日﹣﹣7月11日举行的南非世界杯给无数的球迷留下
Barefoot Traveler is a tour operator that specialises in diving holidays, tailor
石家庄市形成和发展的区位因素是（    ） ①铁路运输的发
2009年8月14日起，公安部在全国全面开展整治酒后驾驶交通违
20. 某学校生物兴趣小组用伊乐藻进行光合作用的实验，将一
14．阅读下面的文字，根据要求作文。 作为一种道德修养，
（江苏省黄桥中学2010届高三上学期期中考试）下列各句中，
下列关于实验基本操作的叙述中，正确的是A．胶头滴管加液
唐卡是藏族文化中独具特色的绘画艺术形成，题材内容涉及
近年来，我国 “悟空”暗物质探测卫星、“墨子”量子实验
 — Catherine, I have cleaned the room for you. — Thanks. You ______ it. I
如图所示是银杏树上结的“白果”，对白果是银杏种子的描
               ，雪上空留马行处。
.设函数的定义域为，的定义域为，则(    ) A.  B.   C.  
“自由钟”是美国独立的象征。它的钟声曾在1776年7月4日和17
生活中常接触到“加碘食盐”、“高钙牛奶”，其中的“碘
下图所示的方法中，属于增大摩擦的是（      ）