已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.
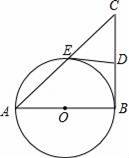

已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.


【考点】切线的判定;圆周角定理.
【分析】先判断出,∠2=∠A,∠3=∠1,进而判断出∠1=∠2,即可判断出△OED≌△OBD即可得出DE⊥OE,即可得出结论.
【解答】解:连接OD,OE,
∵O,D分别是AB,BC中点,
∴OD∥AC,
∴∠2=∠A,∠3=∠1,
∵OA=OE,
∴∠A=∠3,
∴∠1=∠2,
在△OED和△OBD中,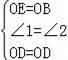
 ,
,
∴△OED≌△OBD,
∴∠OED=∠ABC=90°,
∴DE⊥OE,
∵点D在⊙O上,
∴DE与⊙O相切.
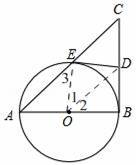

【点评】此题是切线的判定,主要考查了平行线的性质和判定,全等三角形的判定和性质,解本题的关键是判断出,△OED≌△OBD.