（本小题满分12分）
已知函数
图像上点
处的切线与直线
平行（其中
），
（I）求函数
的解析式；
（II）求函数
上的最小值；
（III）对一切
恒成立，求实数t的取值范围。
（本小题满分12分）
已知函数图像上点处的切线与直线平行（其中），
（I）求函数的解析式；
（II）求函数上的最小值；
（III）对一切恒成立，求实数t的取值范围。
解：（I）由点
处的切线方程与直线
平行，得该切线斜率为2，即
又
所以
…………4分
（II）由（I）知
，显然
当
所以函数
上单调递减.当
时
，所以函数
上单调递增，
①
②
时，函数
上单调递增，
因此
…………7分
所以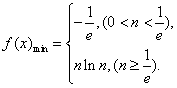
…………10分
（III）对一切
恒成立，又
即
设
则
由
单调递增，
单调递减，
单调递增，
所以
因为对一切恒成立，
故实数t的取值范围为
…………14分