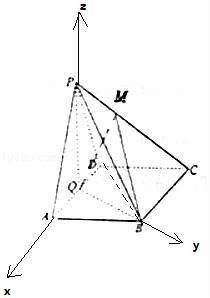
如图，在四棱锥P﹣ABCD中，底面ABCD为菱形，∠BAD=60°，Q是AD的中点．
（1）若PA=PD，求证：平面PQB⊥平面PAD；
（2）若平面APD⊥平面ABCD，且PA=PD=AD=2，点M在线段PC上且满足PC=3PM，求二面角M﹣BQ﹣C的大小．
如图，在四棱锥P﹣ABCD中，底面ABCD为菱形，∠BAD=60°，Q是AD的中点．
（1）若PA=PD，求证：平面PQB⊥平面PAD；
（2）若平面APD⊥平面ABCD，且PA=PD=AD=2，点M在线段PC上且满足PC=3PM，求二面角M﹣BQ﹣C的大小．
【考点】二面角的平面角及求法；平面与平面垂直的判定．
【分析】（1）推导出PQ⊥AD，∴BQ⊥AD，从而AD⊥平面PBQ，由此能证明平面PQB⊥平面PAD．
（2）以Q为原点，QA为x轴，QB为y轴，QP为z轴，建立空间直角坐标系，利用向量法能求出二面角M﹣BQ﹣C的大小．
【解答】证明：（1）∵在四棱锥P﹣ABCD中，底面ABCD为菱形，
∠BAD=60°，Q是AD的中点．
PA=PD，
∴BD=AD=AB，PQ⊥AD，∴BQ⊥AD，
∵PQ∩BQ=Q，∴AD⊥平面PBQ，
∵AD⊂平面PAD，∴平面PQB⊥平面PAD．
解：（2）∵平面APD⊥平面ABCD，且PA=PD=AD=2，点M在线段PC上且满足PC=3PM，
∴以Q为原点，QA为x轴，QB为y轴，QP为z轴，建立空间直角坐标系，
Q（0，0，0），B（0，
，0），P（0，0，），C（﹣2，，0），M（﹣
，
，
），
=（0，
，0），
=（﹣
，
，
），
设平面BQM的法向量
=（x，y，z），
则
，取z=1，得
=（
），
平面BQC的法向量
=（0，0，1），
设二面角M﹣BQ﹣C的平面角为θ，
则cosθ=
=
，θ=60°，
∴二面角M﹣BQ﹣C的大小为60°．
【点评】本题考查面面垂直的证明，考查二面角的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．