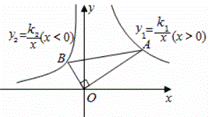
在平面直角坐标系中，点
是双曲线
上任意一点，连接
，过点
作的垂线与双曲线
交于点
，连接
．已知
，则
（ ）
A．
B．
C．
D．
在平面直角坐标系中，点是双曲线上任意一点，连接，过点作的垂线与双曲线交于点，连接．已知，则（ ）
A． B． C． D．
B
【解析】
分别作AE⊥x轴，BF⊥x轴，垂足分别为E，F，证明△AOE∽△OBF得到
，结合反比例函数的系数的几何意义即可得到答案．
【详解】
解：过A作AE⊥x轴，过B作BF⊥x轴，垂足分别为E，F，如图，
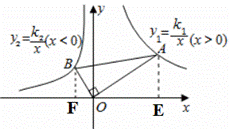
则∠AEO=∠BFO=90°，
∴∠AOE+∠OAE=90°，
∵∠AOB=90°，
∴∠BOF+∠AOE=90°，
∴∠OAE=∠BOF，
∴△AOE∽△OBF，
∴
，
∴
∵
，
，
∴
．
故选：B．
【点睛】
本题主要考查反比例函数系数的几何意义及相似三角形的判定与性质、三角形的面积，利用相似三角形的判定与性质表示出
是解题的关键．