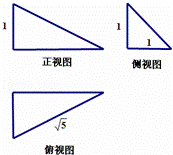
某几何体的三视图(均为直角三角形)及其尺寸如图所示,则该几何体的体积为( )
|
| A. |
| B. |
| C. |
| D. | 1 |
某几何体的三视图(均为直角三角形)及其尺寸如图所示,则该几何体的体积为( )

|
| A. |
| B. |
| C. |
| D. | 1 |
考点:
由三视图求面积、体积.
专题:
空间位置关系与距离.
分析:
先根据三视图判断出几何体的形状及长度关系,然后利用棱锥的体积公式求出几何体的体积.
解答:
解:由三视图知,
该几何体为底面为直角边长分别为1和2的直角三角形,一条侧棱垂直底面,几何体的高为1,
∴该几何体的体积为V=![]() Sh=
Sh=![]() ×
×![]() ×1×2×1=
×1×2×1=![]()
故选B.
点评:
解决三视图的题目,关键是由三视图判断出几何体的形状及度量长度,然后利用几何体的面积及体积公式解决.