在△ABC中，AB=AC=8，作AB边的垂直平分线交AB边于点D，交直线AC于点E，若DE=3，则线段CE的长为 ．
在△ABC中，AB=AC=8，作AB边的垂直平分线交AB边于点D，交直线AC于点E，若DE=3，则线段CE的长为 ．
3或13 ．
【考点】线段垂直平分线的性质；等腰三角形的性质．
【专题】分类讨论．
【分析】分直线DE与线段AC交于E和直线DE与线段CA的延长线交于E两种情况，根据线段的垂直平分线的性质解答即可．
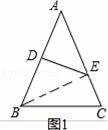
【解答】解：如图1，当直线DE与线段AC交于E时，连接EB，
∵DE是AB边的垂直平分线，
∴∠ADE=90°，AD=
AB=4，又DE=3，
由勾股定理得，AE=5，
则CE=AC﹣AE=3；
如图2，当直线DE与线段CA的延长线交于E时，连接EB，
∵DE是AB边的垂直平分线，
∴∠ADE=90°，AD=AB=4，又DE=3，
由勾股定理得，AE=5，
则CE=AC+AE=13，
故答案为：3或13．
【点评】本题考查的是线段的垂直平分线的性质，线段的垂直平分线上的点到线段的两个端点的距离相等．