（12分）如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，点D为AC边上一点，且AD

（12分）如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，点D为AC边上一点，且AD=3cm，动点E从点A出发，以1cm/s的速度沿线段AB向终点B运动，运动时间为x s．作∠DEF=45°，与边BC相交于点F．设BF长为ycm．
【小题1】（1）当x=   ▲ s时，DE⊥AB；
【小题2】（2）求在点E运动过程中，y与x之间的函数关系式及点F运动路线的长；
【小题3】（3）当△BEF为等腰三角形时，求x的值．

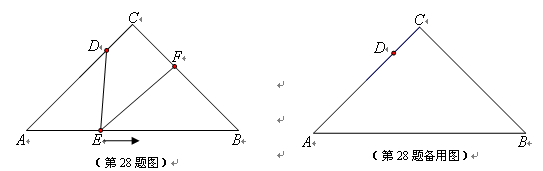
【小题1】（1）
【小题2】（2）∵在△ABC中，∠C=90°，AC=BC=4．
∴∠A＝∠B＝45°，AB=4，∴∠ADE＋∠AED＝135°；
又∵∠DEF＝45°，∴∠BEF＋∠AED＝135°，∴∠ADE＝∠BEF；
∴△ADE∽△BEF···················································································· 4分
∴＝，
∴＝，∴y＝－x²+x························································ 5分
∴y＝－x²+x＝－( x－2)²+
∴当x＝2时，y有最大值＝·································································· 6分
∴点F运动路程为cm············································································ 7分
 
【小题3】（3）这里有三种情况：
①如图，若EF＝BF，则∠B＝∠BEF；
又∵△ADE∽△BEF，∴∠A＝∠ADE＝45°
∴∠AED＝90°，∴AE＝DE＝，
∵动点E的速度为1cm/s，∴此时x＝s；
②如图，若EF＝BE，则∠B＝∠EFB；
又∵△ADE∽△BEF，∴∠A＝∠AED＝45°
∴∠ADE＝90°，∴AE＝3，
∵动点E的速度为1cm/s
∴此时x＝3s；
 
③如图，若BF＝BE，则∠FEB＝∠EFB；
又∵△ADE∽△BEF，∴∠ADE＝∠AED
∴AE＝AD＝3，
∵动点E的速度为1cm/s
∴此时x＝3s；
综上所述，当△BEF为等腰三角形时，x的值为s或3s或3s．
（注：求对一个结论得2分，求对两个结论得4分，求对三个结论得5分）解析:
略