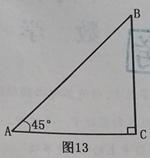
)如图13，已知Rt△ACB中，∠C＝90°，∠BAC＝45°．
（1）（4分）用尺规作图，：在CA的延长线上截取AD＝AB，并连接
BD（不写作法，保留作图痕迹）
（2）（4分）求∠BDC的度数．
（3）（4分）定义：在直角三角形中，一个锐角A的邻边与对边的比叫
做∠A的余切，记作cotA，即
，根据定义，利
用图形求cot22.5°的值．
)如图13，已知Rt△ACB中，∠C＝90°，∠BAC＝45°．
（1）（4分）用尺规作图，：在CA的延长线上截取AD＝AB，并连接
BD（不写作法，保留作图痕迹）
（2）（4分）求∠BDC的度数．
（3）（4分）定义：在直角三角形中，一个锐角A的邻边与对边的比叫
做∠A的余切，记作cotA，即，根据定义，利
用图形求cot22.5°的值．
、解：（1）如图，
（2）∵AD=AB，
∴∠ADB=∠ABD，
而∠BAC=∠ADB+∠ABD，
∴∠ADB
=
∠BAC=×45°=22.5°，
即∠BDC的度数为22.5°；
（3）设AC=x，
∵∠C=90°，∠BAC=45°，
∴△ACB为等腰直角三角形，
∴BC=AC=x，AB=
AC=x，
∴AD=AB=x，
∴CD=x+x=（+1）x，
在Rt△BCD中，cot∠BDC=
=
=
+1，
即cot22.5°=+1．