设点P在曲线y＝
ex上，点Q在曲线y＝ln(2x)上，则|PQ
|的最小值为 ( )
A．1－ln2 B.
(1－ln2)
C．1＋ln2 D.(1＋ln2)
设点P在曲线y＝ex上，点Q在曲线y＝ln(2x)上，则|PQ|的最小值为 ( )
A．1－ln2 B.(1－ln2)
C．1＋ln2 D.(1＋ln2)
B
解析 y＝ex与y＝ln(2x)互为反函数，图像关于y＝x对称．y＝ex上的点P(x，ex)到直线y＝x距离为d＝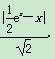
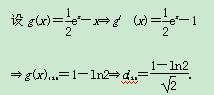由图像关于y＝x对称，得|PQ|最小值为2dmin＝(1－ln2)
亦可用y＝ex在P(x0，ex)处切线斜率为1来建立等式关系．进而求解．