(1)若g(x)=xf(x),f(x)与g(x)在x为某值时,都取得极值,求a的值.
(2)对于给定的负数a,有一个最大的正数M(a),使得x∈[0,M(a)]时,恒有|f(x)|≤5.
求:①M(a)的表达式;
②M(a)的最大值及相应的a值.
(1)若g(x)=xf(x),f(x)与g(x)在x为某值时,都取得极值,求a的值.
(2)对于给定的负数a,有一个最大的正数M(a),使得x∈[0,M(a)]时,恒有|f(x)|≤5.
求:①M(a)的表达式;
②M(a)的最大值及相应的a值.
解析:(1)易知a≠0,f(x)在x=-![]()
∵g(x)=ax3+8x2+3x,
∴g′(x)=3ax2+16x+3.
由题意得
3a(-![]()
∴a=![]()
(2)∵a<0,f(x)=a(x+![]()
∴f(x)max=3-![]()
图(1)
图(2)
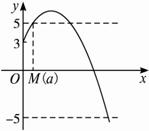
如图(1),当3-![]()
![]()
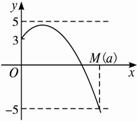
如图(2),当3-![]()
![]()
综上,得M(a)=
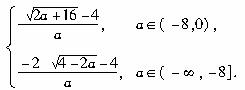
当a∈(-8,0)时,M(a)=
![]()
当a∈(-∞,-8]时,M(a)=![]()
∴当且仅当a=-8时,M(a)有最大值![]()