某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
解析
:利用条件画出线性区域,是解决此类问题的核心.解
:设投资人分别用x万元、y万元投资甲、乙两个项目,由题意知
目标函数z=x+0.5y.
上述不等式组表示的平面区域如下图所示,阴影部分(含边界)即可行域.
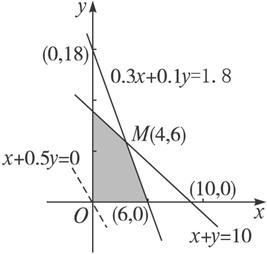
作直线l0:x+0.5y=0,并作平行于直线l0的一组直线x+0.5y=z,z∈R
与可行域相交,其中有一条直线经过可行域上的M点,z值最大,这里M点是直线x+y=10和0.3x+0.1y=1.8的交点.解方程组![]() 得x=4,y=6.
得x=4,y=6.
此时z=4+0.5×6=7(万元).
∵7>0,∴当x=4,y=6时z取得最大值.
∴投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8万元的前提下,使可能的盈利最大.
温馨提示
简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题目是以什么实际问题提出,其解题步骤为:
(1)寻求线性约束条件与线性目标函数;
(2)由二元一次不等式表示的平面区域作出可行域;
(3)在可行域内求目标函数的最优解.