,
,
,…,
,…,计算S1,S2,S3,S4,根据计算结果,猜想Sn的表达式,并用数学归纳法进行证明. 
,,,…,,…,计算S1,S2,S3,S4,根据计算结果,猜想Sn的表达式,并用数学归纳法进行证明. 分析：本题考查观察、分析、归纳、发现规律的能力,考查数学归纳法在等式证明中的应用.在用观察法求数列的通项公式时,要注意观察项与项数的关系.
解：S1==;
S2=+=
;
S3=
+
=
;
S4=
+
=
.
可以看到,上面表示四个结果的分数中,分子与项数n一致,分母可用项数n表示为3n+1.于是可以猜想
.
下面我们用数学归纳法证明这个猜想.
(1)当n=1时,左边=S1=
,
右边=
=
=
,
猜想成立.
(2)假设当n=k(k∈N*)时猜想成立,即
+
+
+…+
=
,
那么, 
+
+
+…+
+
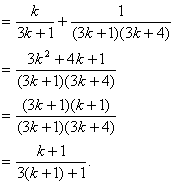
所以,当n=k+1时猜想也成立.
根据(1)、(2),可知猜想对任何n∈N*都成立.