如图,矩形![]() 所在的半平面和直角梯形
所在的半平面和直角梯形![]() 所在的半平面成
所在的半平面成![]() 的二面角,
的二面角,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)在线段![]() 上求一点
上求一点![]() ,使锐二面角
,使锐二面角![]() 的余弦值为
的余弦值为![]() .
.
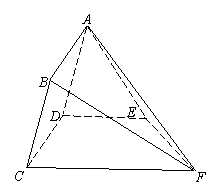
如图,矩形![]() 所在的半平面和直角梯形
所在的半平面和直角梯形![]() 所在的半平面成
所在的半平面成![]() 的二面角,
的二面角,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)在线段![]() 上求一点
上求一点![]() ,使锐二面角
,使锐二面角![]() 的余弦值为
的余弦值为![]() .
.

(Ⅰ)因为![]() ∥
∥![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() ,
,
同理![]() ∥平面
∥平面![]() ,又因为
,又因为![]() ,所以平面
,所以平面![]() ∥平面
∥平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() . ………………………………………5分
. ………………………………………5分
(Ⅱ)因为![]() ,
,![]() 所以
所以![]() 就是二面角
就是二面角![]() 的平面角,为
的平面角,为![]() , ……………………………………………………………………………………6分
, ……………………………………………………………………………………6分
又![]() ,所以
,所以![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
 作
作![]() 于
于![]() ,则
,则![]() ,…………7分
,…………7分
连结![]() ,在
,在![]() 中由余弦定理求得
中由余弦定理求得![]() ,
,
易求得,![]() ,
,![]() ,
,![]() ,
,![]() . ……………………………………………8分
. ……………………………………………8分
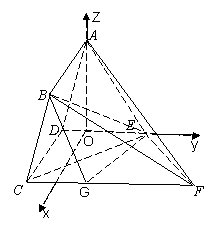
以![]() 为原点,以平行于
为原点,以平行于![]() 的直线为
的直线为![]() 轴,以直线
轴,以直线![]() 为
为
![]() 轴,建立如图空间直角坐标系
轴,建立如图空间直角坐标系![]() ,
,
则![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设![]() ,
,
则![]() ,
,![]() ,
,
设平面![]() 的一个法向量为,
的一个法向量为,![]() ,
,
则由  得,
得,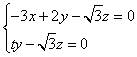 ,
,
取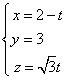 得,
得, ![]() , …………………………………………10分
, …………………………………………10分
平面![]() 的一个法向量
的一个法向量![]() , …………………………………………11分
, …………………………………………11分
所以,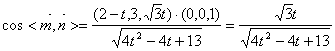 , ………12分
, ………12分
为使锐二面角![]() 的余弦值为
的余弦值为![]() ,只需
,只需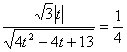 ,
,
解得![]() ,此时
,此时![]() , …………………………………………………13分
, …………………………………………………13分
即所求的点![]() 为线段
为线段![]() 的靠近
的靠近![]() 端的四分之一分点. …………………………14分
端的四分之一分点. …………………………14分