设f（x）=xex（e为自然对数的底数），g（x）=（x+1）2． （I）记，讨

设f（x）=xe^x（e为自然对数的底数），g（x）=（x+1）²．

（I）记，讨论函F（x）单调性；

（II）令G（x）=af（x）+g（x）（a∈R），若函数G（x）有两个零点．

（i）求参数a的取值范围；

（ii）设x₁，x₂是G（x）的两个零点，证明x₁+x₂+2＜0．

【考点】利用导数研究函数的单调性；根的存在性及根的个数判断．

【分析】（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可；

（Ⅱ）（i）求出函数的导数，通过讨论a的范围，根据函数的零点的个数，求出a的范围即可；

（ii）根据a的范围，得到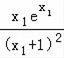==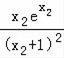﹣，令m＞0，得到F （=1+m）﹣F（﹣1﹣m）=（e^2m+1），再令φ（m）=e^2m+1，根据函数的单调性证明即可．

【解答】解：（Ⅰ）F（x）==，（x≠﹣1），

F′（x）==，

∴x∈（﹣∞，﹣1）时，F′（x）＜0，F（x）递减，

x∈（﹣1，+∞）时，F′（x）＞0，F（x）递增；

（Ⅱ）由已知，G（x）=af（x）+g（x）=axe^x+（x+1）²，

G′（x）=a（x+1）e^x+2（x+1）=（x+1）（ae^x+2），

（i）①a=0时，G（x）=（x+1）²，有唯一零点﹣1，

②a＞0时，ae^x+2＞0，

∴x∈（﹣∞，﹣1）时，G′（x）＜0，G（x）递减，

x∈（﹣1，+∞）时，G′（x）＞0，G（x）递增，

∴G（x）_极小值=G（﹣1）=﹣＜0，

∵G（0）=1＞0，∴x∈（﹣1，+∞）时，G（x）有唯一零点，

x＜﹣1时，ax＜0，则e^x＜，∴axe^x＞，

∴G（x）＞+（x+1）²=x²+（2+）x+1，

∵△=﹣4×1×1=+＞0，

∴∃t₁，t₂，且t₁＜t₂，当x∈（﹣∞，t₁），（t₂，+∞）时，

使得x²+（2+）x+1＞0，

取x₀∈（﹣∞，﹣1），则G（x₀）＞0，则x∈（﹣∞，﹣1）时，G（x）有唯一零点，

即a＞0时，函数G（x）有2个零点；

③a＜0时，G′（x）=a（x+1）（e^x﹣（﹣）），

由G′（x）=0，得x=﹣1或x=ln（﹣），

若﹣1=ln（﹣），即a=﹣2e时，G′（x）≤0，G（x）递减，至多1个零点；

若﹣1＞ln（﹣），即a＜﹣2e时，G′（x）=a（x+1）（e^x﹣（﹣）），

注意到y=x+1，y=e^x+都是增函数，

∴x∈（﹣∞，ln（﹣））时，G′（x）＜0，G（x）是减函数，

x∈（ln（﹣），﹣1）时，G′（x）＞0，G（x）递增，

x∈（﹣1，+∞）时，G′（x）＜0，G（x）递减，

∵G（x）极小值=G（ln（﹣））=ln²（﹣）+1＞0，

∴G（x）至多1个零点；

若﹣1＜ln（﹣），即a＞﹣2e时，

x∈（﹣∞，﹣1）时，G′（x）＜0，G（x）是减函数，

x∈（﹣1，ln（﹣））时，G′（x）＞0，G（x）递增，

x∈（ln（﹣），+∞）时，G′（x）＜0，G（x）递减，

∵G（x）极小值=G（﹣1）=﹣＞0，

∴G（x）至多1个零点；

综上，若函数G（x）有2个零点，

则参数a的范围是（0，+∞）；

（ii）由（i）得：函数G（x）有2个零点，则参数a的范围是（0，+∞），

x₁，x₂是G（x）的两个零点，则有：

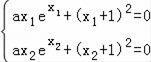，即，即==﹣，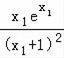

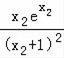∵F（x）=，则F（x₁）=F（x₂）＜0，且x₁＜0，x₁≠﹣1，x₂＜0，x₂≠﹣1，x₁≠x₂，

由（Ⅰ）知，当x∈（﹣∞，﹣1）时，F（x）是减函数，x∈（﹣1，+∞）时，F（x）是增函数，

令m＞0，F （=1+m）﹣F（﹣1﹣m）=（e^2m+1），

再令φ（m）=e^2m+1=e^2m﹣﹣1，

则φ′（m）=＞0，

∴φ（m）＞φ（0）=0，又＞0，

m＞0时，F（﹣1+m）﹣F（﹣1﹣m）＞0恒成立，

即F（﹣1+m）＞F（﹣1﹣m）恒成立，

令m=﹣1﹣x₁＞0，即x₁＜﹣1，有F（﹣1+（﹣1﹣x₁））＞F（﹣1﹣（﹣1﹣x₁）），

即F（﹣2﹣x₁）＞F（x₁）=F（x₂），

∵x₁＜﹣1，∴﹣2﹣x₁＞﹣1，又F（x₁）=F（x₂），必有x₂＞﹣1