如图，点I为△ABC的内心，点O为△ABC的外心，∠O＝140°，则∠I为（ �

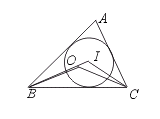
如图，点I为△ABC的内心，点O为△ABC的外心，∠O＝140°，则∠I为（）

（A）140° （B）125° （C）130° （D）110°

答案

因点O为△ABC的外心，则∠BOC、∠A分别是所对的圆心角、圆周角，所以∠O＝2∠A，故∠A＝×140°＝70°．又因为I为△ABC的内心，所以∠I＝90°＋∠A＝90°＋×70°＝125°．

【答案】B．

【

下列关于文学常识的表述有误的一组是（） A．苏轼，北宋文学家、书画家，字子瞻，号东坡居士，与其父苏洵、其弟苏辙合称“三苏”，同列于唐

一辆轿车违章超车，以108km/h的速度驶入左侧逆行道时，猛然发现正前方80m处一辆卡车正以72km/h的速度迎面驶来，两车司机同时刹车，刹车加速度大小都

下列各句中翻译不正确的一句是（） A 他日趋庭，叨陪鲤对；今兹捧袂，喜托龙门。译文：过些日子，（我将到父亲身边），一定要像孔鲤那样接受父

沸腾是在液体和液体内部同时进行的汽化现象。

将紫色洋葱在完全营养液中浸泡一段时间，撕取外表皮，先用浓度为0.3g/mL的蔗糖溶液处理，细胞发生质壁分离后，立即将外表皮放入蒸馏水中，直到细

2008年12月，中国外交部部长杨洁篪在北京说，中日关系通过两国领导人的“破冰”、“融冰”和“迎春”、“暖春”之旅，已经回到了正常的发展轨道

李嘉图认为，商品价格的波动使资本恰好按照必要的数量运行，在没有政府的干预时，农业、商业和制造业最为繁荣，需要国家做的全部事情就是避免

如图，直线y=﹣x+m与y=nx+4n（n≠0）的交点的横坐标为﹣2，则关于x的不等式﹣x+m＞nx+4n＞0的整数解为（）A．﹣1B．﹣5C．﹣4D．﹣3