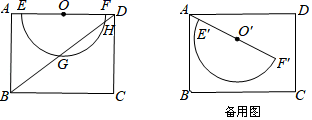
如图，在矩形ABCD中，AB＝6，BC＝8，O是AD的中点，以O为圆心在AD的下

如图，在矩形ABCD中，AB＝6，BC＝8，O是AD的中点，以O为圆心在AD的下方作半径为3的半圆O，交AD于E、F．

思考：连接BD，交半圆O于G、H，求GH的长；

探究：将线段AF连带半圆O绕点A顺时针旋转，得到半圆O′，设其直径为E'F′，旋转角为α（0＜α＜180°）．

（1）设F′到AD的距离为m，当m＞时，求α的取值范围；

（2）若半圆O′与线段AB、BC相切时，设切点为R，求的长．

（sin49°＝，cos41°＝，tan37°＝，结果保留π）

思考：GH＝ ；探究：（1）α的取值范围为30^°＜α＜150^°；（2）或.

【解析】

思考：作ON⊥BD，证△ADB∽△NDO得，据此求得ON＝，再根据勾股定理求得NH的长，继而由GH＝2NH可得答案；

探究：(1)过F′作F′Q⊥AD于Q，分垂足Q落在线段AD上和线段DA延长线上两种情况，利用Rt△AQF′中，sin∠QAF′＝求得∠QAF′的度数即可得出∠α的范围；

(2)分半圆O′与AB相切和与BC相切两种情况求解，求出所对圆心角度数即可得出答案．

【详解】

思考：如图1，过O作ON⊥BD于N，

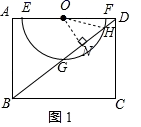
∴HN＝GN，

∵四边形ABCD是矩形，

∴AD＝BC＝8，∠BAD＝90°，

又∵AB＝6，

∴BD＝10，

∵∠BAD＝∠OND＝90°，∠ADB＝∠NDO，

∴△ADB∽△NDO，

∴，

∴ON＝，

连接OH，

∵OH＝3，

∴HN＝，

∴GH＝2HN＝；

探究：(1)如图2，过F′作F′Q⊥AD于Q，

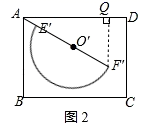
当F′到AD的距离为时，有F′Q＝，

此时，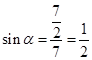

所以α＝30°，

如图3，当Q落在DA延长线时，

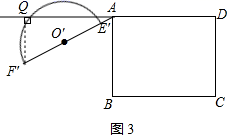
可求得α＝150^°，

所以当m＞时，α的取值范围为30^°＜α＜150^°；

(2)如图4，当半圆O′与AB相切，切点为R，连接O′R，

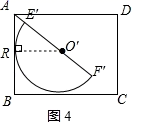
∴∠O′RA＝90°，

∵，

∴∠O′AR＝49°，

∴∠F′O′R＝90°+49°＝139°，

∴的长＝；

如图5，当半圆O′与BC相切，切点为R，过点O′作O′P⊥AB于P，连接O′R，

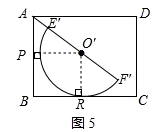
∴∠O′RB＝90°，

易得四边形PBRO′是矩形，

∴O′R＝BP＝3，

∴AP＝3，

∴，

∴∠PO'A＝49°，

∴∠RO'F'＝41°，

∴的长＝，

综上，的长为或.

【点睛】

本题主要考查圆的综合问题，解题的关键是掌握垂径定理、相似三角形的判定与性质、矩形的判定与性质及切线的性质等知识点．