（本小题共14分）
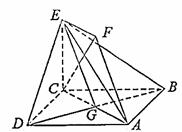如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC,EF∥AC,AB=
，CE=EF=1.
（Ⅰ）求证：AF∥平面BDE；
（Ⅱ）求证：CF⊥平面BDE；
（Ⅲ）求二面角A-BE-D的大小。
（本小题共14分）
如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC,EF∥AC,AB=，CE=EF=1.
（Ⅰ）求证：AF∥平面BDE；
（Ⅱ）求证：CF⊥平面BDE；
（Ⅲ）求二面角A-BE-D的大小。
证明：（I）设AC与BD交于点G，因为EF∥AG，且EF=1，AG=
AC=1，所以四边形AGEF为平行四边形。所以AF∥EG。因为EG
P平面BDE，AF
平面BDE，所以AF∥平面BDE。
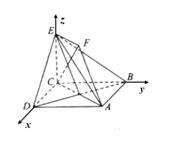（II）因为正方形ABCD和四边形ACEF所在的平面互相垂直，且CE⊥AC，所以CE⊥AC，所以CE⊥平面ABCD。如图，以C为原点，建立空间直角坐标系C-xyz。则C（0， 0， 0），A（
，，0），D（，0， 0），E（0， 0， 1），F（
，，1）。所以
=（，，1），
=（0，－，１），
＝（－，0，１）。所以·= 0-1+1=0，·=－１＋０＋１＝０。所以CF⊥BE，CF⊥DE，所以CF⊥平面BDE
（III）由（II）知，=（，，1），是平面BDE的一个法向量，设平面ABE的法向量
=（x,y,z）,则·
=0，·=0。
即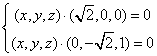
所以x=0，且z=y。令y=1，则z=。所以n=（
），从而cos（，）=
因为二面角A-BE-D为锐角，所以二面角A-BE-D为
。