如图，抛物线
与
轴相交于点
和点
，与
轴相交于点
，作直线
．
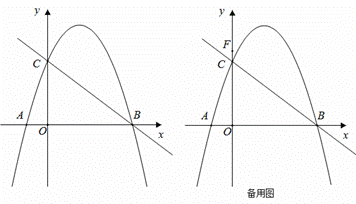
（1）求抛物线的解析式；
（2）在直线上方的抛物线上存在点
，使
，求点的坐标；
（3）在（2）的条件下，点
的坐标为
，点
在抛物线上，点
在直线上，当以
为顶点的四边形是平行四边形时，请直接写出点的坐标．
如图，抛物线与轴相交于点和点，与轴相交于点，作直线．
（1）求抛物线的解析式；
（2）在直线上方的抛物线上存在点，使，求点的坐标；
（3）在（2）的条件下，点的坐标为，点在抛物线上，点在直线上，当以为顶点的四边形是平行四边形时，请直接写出点的坐标．
（1）
；（2）点坐标为
；（3）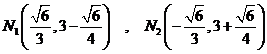
，
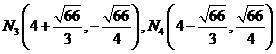
【解析】
（1）将A、C点坐标分别代入抛物线中，联立即可求得a和c的值，从而求出抛物线解析式；
（2）过点
作
轴交抛物线于点
，则
，过点作
交抛物线于点，设
，借助
，即可求得t的值，从而求得D点坐标；
（3）先求出直线BC的解析式，设
，分DF为边和DF为对角线两种情况讨论，表示出M点坐标，代入抛物线中求得n的值，即可得出N点坐标．
【详解】
解：（1）：抛物线
经过点
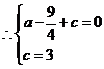，解得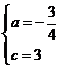
∴抛物线的解析式为
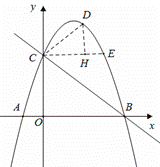
（2）过点作轴交抛物线于点，则
过点作交抛物线于点
过点作
于点
，则
设点的横坐标为
，则
∵点是与轴的交点
，
解得
的坐标为
，
解得
（舍去），
∴点的纵坐标为：
则点坐标为
（3）设直线BC的解析式为：
，
将C（0,3），B（4，0）分别代入得，
，解得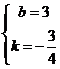
，
∴直线BC的解析式为：
，
设，
①当FD为平行四边形的边时，
如图，当N点在M点左侧时，
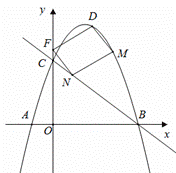
则
整理得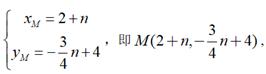
故
，
解得：
，
此时；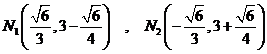
同理当N点在M点右侧时可得
，
故
，
解得
，
此时；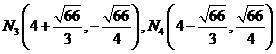
①当FD为平行四边形的对角线时，
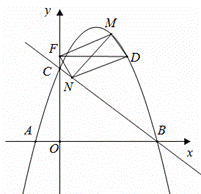
则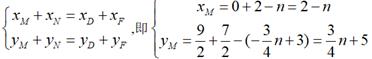
故
，整理得
，
该方程无解．
综上所述：，．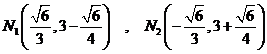
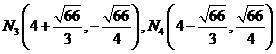【点睛】
本题考查二次函数综合，分别考查了求二次函数解析式，相似三角形的性质，和二次函数与平行四边形问题．（1）中直接代入点的坐标即可，难度不大；（2）中能正确作辅助线，构造相似三角形是解题关键；（3）中能分类讨论是解题关键，需注意平行四边形对边平行且相等，可借助这一点结合图象表示M点坐标．