.（1）判定函数f(x)的单调性;
（2）设a＞1,证明
＜
.
.（1）判定函数f(x)的单调性;
（2）设a＞1,证明＜.
解：(1)∵f′(x)=-=-
=
-
=
=-
.
又∵函数f(x)的定义域为x＞0,
∴
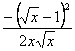≤0.
而在(0，+∞)上，只有当x=1时，f′(x)=0,
∴f(x)是定义域上的减函数.
(2)由(1)f(x)是定义域上的减函数，
∴当a＞1时,f(a)＜f(1),
即lna-
＜0,即lna＜
.又∵a-1＞0,
∴
＜
成立.