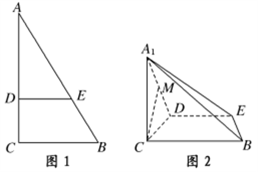
如图1，在Rt△ABC中，∠C＝90°，BC＝3，AC＝6，D，E分别是AC，AB上的点

如图1，在Rt△ABC中，∠C＝90°，BC＝3，AC＝6，D，E分别是AC，AB上的点，且DE∥BC，DE＝2．将△ADE沿DE折起到△A₁DE的位置，使A₁C⊥CD，如图2．                

(1)求证：A₁C⊥平面BCDE；

(2)若M是A₁D的中点，求CM与平面A₁BE所成角的大小；

(3)线段BC上是否存在点P，使平面A₁DP与平面A₁BE垂直？说明理由．

【解析】试题分析：（1）证明A₁C⊥平面BCDE，因为A₁C⊥CD，只需证明A₁C⊥DE，即证明DE⊥平面A₁CD；

（2）建立空间直角坐标系，用坐标表示点与向量，求出平面A₁BE法向量，=（﹣1，0，），利用向量的夹角公式，即可求得CM与平面A₁BE所成角的大小；

（3）设线段BC上存在点P，设P点坐标为（0，a，0），则a∈，求出平面A₁DP法向量为

假设平面A₁DP与平面A₁BE垂直，则，可求得0≤a≤3，从而可得结论．

（1）证明：∵CD⊥DE，A₁D⊥DE，CD∩A₁D=D，

∴DE⊥平面A₁CD，

又∵A₁C⊂平面A₁CD，∴A₁C⊥DE

又A₁C⊥CD，CD∩DE=D

∴A₁C⊥平面BCDE

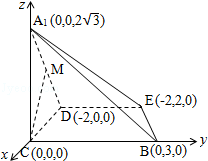
（2）解：如图建系，则C（0，0，0），D（﹣2，0，0），A₁（0，0，2），B（0，3，0），E（﹣2，2，0）

∴，

设平面A₁BE法向量为

则∴∴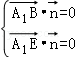

∴

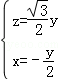
又∵M（﹣1，0，），∴=（﹣1，0，）

∴

∴CM与平面A₁BE所成角的大小45°

（3）解：设线段BC上存在点P，设P点坐标为（0，a，0），则a∈

∴，

设平面A₁DP法向量为

则∴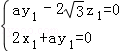

∴

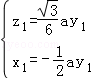
假设平面A₁DP与平面A₁BE垂直，则，

∴3a+12+3a=0，6a=﹣12，a=﹣2

∵0≤a≤3

∴不存在线段BC上存在点P，使平面A₁DP与平面A₁BE垂直