某同学在学习等径球最密堆积（立方最密堆积A1和六方最密堆积A3）后，提出了另一种最
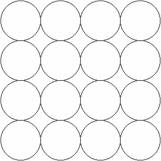密堆积形式Ax 。如右图所示为Ax 堆积的片层形式，然后第二层就堆积在第一层的空隙上。请根据Ax 的堆积形式回答：
（1）计算在片层结构中（如右图所示）球数、空隙数和切点数之比
（2）在Ax 堆积中将会形成正八面体空隙和正四面体空隙。请在片层图中画出正八面体空隙（用・表示）和正四面体空隙（用×表示）的投影，并确定球数、正八面体空隙数和正四面体空隙数之比
（3）指出Ax 堆积中小球的配位数
（4）计算Ax 堆积的原子空间利用率。
（5）计算正八面体和正四面体空隙半径（可填充小球的最大半径，设等径小球的半径为r）。
（6）已知金属Ni晶体结构为Ax 堆积形式，Ni原子半径为124.6 pm，计算金属Ni的密度。（Ni的相对原子质量为58.70）
（7）如果CuH 晶体中Cu＋的堆积形式为Ax 型，H－ 填充在空隙中，且配位数是4。则H－ 填充的是哪一类空隙，占有率是多少？
（8）当该同学将这种Ax 堆积形式告诉老师时，老师说Ax 就是A1或A3的某一种。你认为是哪一种，为什么？
（1）112 一个球参与四个空隙，一个空隙由四个球围成；一个球参与四个切点，一个切点由二个球共用。
（2）图略，正八面体中心投影为平面◇空隙中心，正四面体中心投影为平面切点 112 一个球参与六个正八面体空隙，一个正八面体空隙由四个球围成；一个球参与八个正四面体空隙，一个正四面体空隙由四个球围成。
（3）小球的配位数为12 平面已配位4个，中心球周围的四个空隙上下各堆积4个，共12个。
（4）74.05% 以4个相邻小球中心构成底面，空隙上小球的中心为上底面的中心构成正四棱柱，设小球半径为r，则正四棱柱边长为2 r，高为
r，共包括1个小球（4个1/4，1个1/2），空间利用率为
（5）正八面体空隙为0.414 r，正四面体空隙为0.225 r。
（6）8.91g/cm3 根据第（4）题，正四棱柱质量为58.70 / NA g，体积为1.094×10－23cm3。
（7）H－ 填充在正四面体空隙，占有率为50% 正四面体为4配位，正八面体为6配位，且正四面体空隙数为小球数的2倍。
（8）Ax 就是A1，取一个中心小球周围的4个小球的中心为顶点构成正方形，然后上面再取两层，就是顶点面心的堆积形式。底面一层和第三层中心小球是面心，周围四小球是顶点，第二层四小球（四个空隙上）是侧面心。 也可以以相邻四小球为正方形边的中点（顶点为正八面体空隙），再取两层，构成与上面同样大小的正方体，小球位于体心和棱心，实际上与顶点面心差1/2单位。