已知数列{an}的前n项和Sn=n2+n，那么它的通项公式为an= ．
已知数列{an}的前n项和Sn=n2+n，那么它的通项公式为an= ．
考点：
等差数列的前n项和；数列递推式．
专题：
计算题．
分析：
由题意知得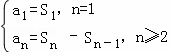 
，由此可知数列{an}的通项公式an．
解答：
解：a1=S1=1+1=2，
an=Sn﹣Sn﹣1=（n2+n）﹣[（n﹣1）2+（n﹣1）]
=2n．
当n=1时，2n=2=a1，
∴an=2n．
故答案为：2n．
点评：
本题主要考查了利用数列的递推公式an=Sn﹣Sn﹣1求解数列的通项公式，属于基础题．