（本题满分16分；第（1）小题5分，第（2）小题5分，第三小题6分）
已知函数 
（1）判断并证明
在
上的单调性；
（2）若存在
，使
，则称为函数
的不动点，现已知该函数有且仅有一个不动点，求
的值；
（3）若
在上恒成立 , 求的取值范围．
（本题满分16分；第（1）小题5分，第（2）小题5分，第三小题6分）
已知函数
（1）判断并证明在上的单调性；
（2）若存在，使，则称为函数的不动点，现已知该函数有且仅有一个不动点，求的值；
（3）若在上恒成立 , 求的取值范围．
略
（1）
对任意的
------------------------------------------- 1分
-------------------------------- 3分
∵
∴
∴
，函数在上单调递增。----------------5分
（2）解：令
，------------------------------------7分
令
（负值舍去）--------------------------------------9分
将
代入
得
--------10分
（3）∵ ∴
----------------------------------------12分
∵
∴
（等号成立当
）--------------------14分
∴
的取值范围是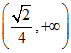
-------- 16分