双曲线C:
-
=1(a>0,b>0)的右焦点为F(c,0),以原点为圆心,c为半径的圆与双曲线在第二象限的交点为A,若此圆在A点处切线的斜率为
,则双曲线C的离心率为 .
双曲线C:-=1(a>0,b>0)的右焦点为F(c,0),以原点为圆心,c为半径的圆与双曲线在第二象限的交点为A,若此圆在A点处切线的斜率为,则双曲线C的离心率为 .
+1解析:如图,由题知∠ABO=30°,
所以∠AOB=60°,OA=c,
设A(x0,y0),
则x0=-c·cos 60°=-
,
y0=csin 60°=
c,
由双曲线定义知
2a=
-
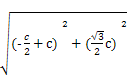
=(-1)c,
∴e=
=+1.