（08年惠州一中一模理） 已知函数
（I）求
在区间
上的最大值
（II）是否存在实数
使得
的图象与
的图象有且只有三个不同的交点？若存在，求出
的取值范围；若不存在，说明理由。
（08年惠州一中一模理） 已知函数
（I）求在区间上的最大值
（II）是否存在实数使得的图象与的图象有且只有三个不同的交点？若存在，求出的取值范围；若不存在，说明理由。
解析：（
当
即
时，
在
上单调递增，
当
即
时，
当
时，在上单调递减，
综上，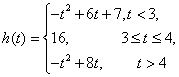
（II）函数
的图象与
的图象有且只有三个不同的交点，即函数
的图象与
轴的正半轴有且只有三个不同的交点。
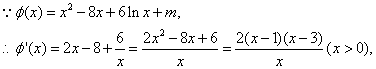
当
时，
是增函数；
当
时，
是减函数；
当
时，是增函数；
当
或
时，
当充分接近0时，
当充分大时，
要使
的图象与轴正半轴有三个不同的交点，必须且只须
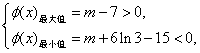即
，使得函数与的图象有且只有三个不同的交点，的取值范围为