已知关于
的一元二次方程
有两个实数根
和
．
（1）求实数
的取值范围；
（2）当
时，求的值．
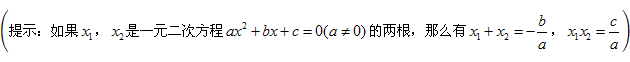
已知关于的一元二次方程有两个实数根和．
（1）求实数的取值范围；
（2）当时，求的值．
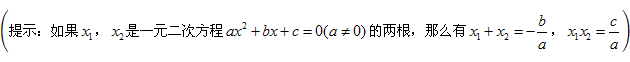
解:（1）∵ 一元二次方程有两个实数根,
∴ 
,∴ 
.
（2）当，即
时，
或
.
当时，依据一元二次方程根与系数的关系可得
,
∴
,∴ 
.
又 由（1）一元二次方程有两个实数根时的取值范围是,知不成立,故无解.
当时，
,方程有两个相等的实数根,
∴ 
,∴ 
.
综上所述,当时，.