如图①,矩形纸片ABCD的边长分别为a、b(a<b),点M、N分别为边AD、
如图①,矩形纸片ABCD的边长分别为a、b(a<b),点M、N分别为边AD、BC上两点(点A、C除外),连结MN.
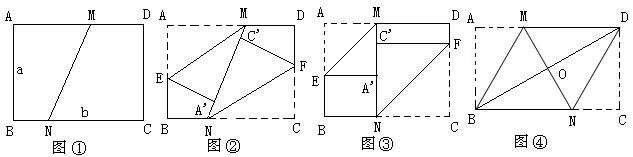
(1)如图②,分别沿ME、NF将MN两侧纸片折叠,使点A、C分别落在MN上的A’、C’处,直接写出ME与FN的位置关系;
(2)如图③,当MN⊥BC时,仍按(1)中的方式折叠,请求出四边形A’EBN与四边形C’FDM
的周长(用含a的代数式表示),并判断四边形A’EBN与四边形C’FDM周长之间的数量关系;
(3)如图④,若对角线BD与MN交于点O,分别沿BM、DN沿ME、NF将MN两侧纸片折叠,折叠后,点A、C恰好都落在点O处,并且得到的四边形BNDM是菱形,请你探索a、b之间的数量关系;
(4)在(3)情况下,当a=
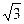
时,求菱形BNDM的面积.
(1)平行
(2)相等
(3)
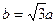
(4)
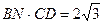
解析:
(1) ME∥FN ………………2分
(2) ∵由折叠得知:A’E=AE, 四边形A’EBN是矩形,
∴四边形A’EBN的周长=2(A’E+EB)=2(AE+EB)=2AB=2a,…3分
同理,四边形C’FDM的周长=2a,
∴四边形A’EBN的周长=四边形C’FDM的周长 ………………4分
(3) ∵△OND是由△CND折叠得到的,
∴OD="CD=a, "
同理,OB=a,
∴BD="2a " ………………6分
在△BCD中,∠C=90°,由勾股定理得,
BC2+CD2=BD2,
∴b2+a2=(2a)2
∴
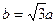
. ………………7分
(4)当a=
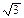
时,CD=
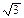
,BC=3
在菱形BNDM中,DN=BN
设DN=BN=x,则CN=3-x .在△DCN中,∠C=90°,由勾股定理得,
NC2+CD2=ND2, ………………8分
∴
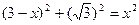
,
解得,
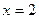
,
∴ 菱形BNDM的面积=
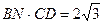
………………9分.
(其它解法可自行参照上述标准给分)
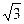 时,求菱形BNDM的面积.
时,求菱形BNDM的面积.

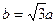
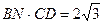 解析:
解析: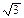 时,CD=
时,CD=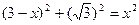 ,
,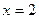 ,
,