жӯЈеӣӣйқўдҪ“пјҲеҚіеӣӣжқЎжЈұеқҮзӣёзӯүзҡ„дёүжЈұй”Ҙпјүзҡ„4дёӘйқўдёҠеҲҶеҲ«еҶҷжңүж•°еӯ—1пјҢ2пјҢ3пјҢ4пјҢе°Ҷ3дёӘиҝҷж ·еӨ§е°ҸзӣёеҗҢгҖҒиҙЁең°еқҮеҢҖзҡ„жӯЈеӣӣйқўдҪ“еҗҢж—¶жҠ•жҺ·дәҺжЎҢйқўдёҠпјҺи®°ОҫдёәдёҺжЎҢйқўжҺҘи§Ұзҡ„3дёӘйқўдёҠзҡ„3дёӘж•°еӯ—дёӯжңҖеӨ§еҖјдёҺжңҖе°ҸеҖјд№Ӣе·®зҡ„з»қеҜ№еҖјпјҢеҲҷйҡҸжңәеҸҳйҮҸОҫзҡ„жңҹжңӣEОҫзӯүдәҺгҖҖгҖҖпјҺ
иҖғзӮ№пјҡ
зҰ»ж•ЈеһӢйҡҸжңәеҸҳйҮҸзҡ„жңҹжңӣдёҺж–№е·®пјҺ | | дё“йўҳпјҡ | жҰӮзҺҮдёҺз»ҹи®ЎпјҺ |
| еҲҶжһҗпјҡ | з”ЁеҲ—дёҫжі•еҫ—еҲ°жүҖжңүеҹәжң¬дәӢ件пјҢжүҫеҮәжүҖжңүжұӮзҡ„еҸҜиғҪдәӢ件еҢ…жӢ¬зҡ„еҹәжң¬дәӢ件еҸҠе…¶жҰӮзҺҮпјҢеҶҚеҲ©з”Ёж•°еӯҰжңҹжңӣзҡ„и®Ўз®—е…¬ејҸеҚіеҸҜеҫ—еҮәпјҺ |
| и§Јзӯ”пјҡ | и§ЈпјҡОҫзҡ„еҸҜиғҪеҸ–еҖјдёә0пјҢ1пјҢ2пјҢ3пјҺдёҺжЎҢйқўжҺҘи§Ұзҡ„3дёӘйқўдёҠзҡ„3дёӘж•°еӯ—е…ұжңү43=64дёӘеҹәжң¬дәӢ件пјҺ в‘ еҪ“дёҺжЎҢйқўжҺҘи§Ұзҡ„3дёӘйқўдёҠзҡ„3дёӘж•°еӯ—зӣёеҗҢж—¶пјҢеҢ…жӢ¬4дёӘеҹәжң¬дәӢ件пјҡпјҲ1пјҢ1пјҢ1пјүпјҢпјҲ2пјҢ2пјҢ2пјүпјҢпјҲ3пјҢ3пјҢ3пјүпјҢ пјҲ4пјҢ4пјҢ4пјүпјҢеҚіОҫ=0=|1п№Ј1|=вҖҰ=|4п№Ј4|пјҢвҲҙPпјҲОҫ=0пјү= пјӣ пјӣ в‘ЎеҪ“дёҺжЎҢйқўжҺҘи§Ұзҡ„3дёӘйқўдёҠзҡ„3дёӘж•°еӯ—зӣёе·®2ж—¶пјҢеҢ…жӢ¬д»ҘдёӢ24дёӘеҹәжң¬дәӢ件пјҡ пјҲ1пјҢ1пјҢ3пјүпјҢпјҲ1пјҢ3пјҢ1пјүпјҢпјҲ3пјҢ1пјҢ1пјүпјҢпјҲ3пјҢ3пјҢ1пјүпјҢпјҲ3пјҢ1пјҢ3пјүпјҢпјҲ1пјҢ3пјҢ3пјүпјҢпјҲ2пјҢ2пјҢ4пјүпјҢпјҲ2пјҢ4пјҢ2пјүпјҢпјҲ4пјҢ2пјҢ2пјүпјҢпјҲ2пјҢ4пјҢ4пјүпјҢпјҲ4пјҢ2пјҢ4пјүпјҢпјҲ4пјҢ4пјҢ2пјүпјҢпјҲ1пјҢ2пјҢ3пјүпјҢвҖҰпјҲ3пјҢ2пјҢ1пјүпјҢпјҲ2пјҢ3пјҢ4пјүпјҢвҖҰпјҲ4пјҢ3пјҢ2пјүпјҢвҲҙPпјҲОҫ=2пјү=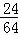 пјӣ пјӣ в‘ўеҪ“дёҺжЎҢйқўжҺҘи§Ұзҡ„3дёӘйқўдёҠзҡ„3дёӘж•°еӯ—зӣёе·®3ж—¶пјҢеҢ…жӢ¬д»ҘдёӢ18дёӘеҹәжң¬дәӢ件пјҡпјҲ1пјҢ1пјҢ4пјүпјҢпјҲ1пјҢ4пјҢ1пјүпјҢпјҲ4пјҢ1пјҢ1пјүпјҢ пјҲ4пјҢ4пјҢ1пјүпјҢпјҲ4пјҢ1пјҢ4пјүпјҢпјҲ1пјҢ4пјҢ4пјүпјҢпјҲ4пјҢ2пјҢ1пјүпјҢпјҲ2пјҢ4пјҢ1пјүпјҢпјҲ4пјҢ1пјҢ2пјүпјҢпјҲ2пјҢ1пјҢ4пјүпјҢпјҲ1пјҢ2пјҢ4пјүпјҢпјҲ1пјҢ4пјҢ2пјүпјҲ4пјҢ3пјҢ1пјүпјҢпјҲ3пјҢ4пјҢ1пјүпјҢпјҲ4пјҢ1пјҢ3пјүпјҢпјҲ3пјҢ1пјҢ4пјүпјҢпјҲ1пјҢ3пјҢ4пјүпјҢпјҲ1пјҢ4пјҢ3пјүпјҺвҲҙPпјҲОҫ=3пјү=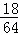 пјӣ пјӣ в‘ЈеҪ“дёҺжЎҢйқўжҺҘи§Ұзҡ„3дёӘйқўдёҠзҡ„3дёӘж•°еӯ—зӣёе·®1ж—¶пјҢPпјҲОҫ=1пјү=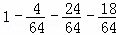 = =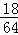 пјҺ пјҺ Оҫзҡ„еҲҶеёғеҲ—еҰӮдёӢиЎЁпјҡ вҲҙEОҫ=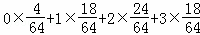 = =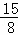 пјҺ пјҺ ж•…зӯ”жЎҲдёә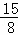 пјҺ пјҺ 
|
| зӮ№иҜ„пјҡ | зҶҹз»ғеҫ—еҲ°жүҖжңүзҡ„еҹәжң¬дәӢ件е’ҢжӯЈзЎ®еҫ—еҲ°еҸҜиғҪдәӢ件еҢ…жӢ¬зҡ„еҹәжң¬дәӢ件еҸҠе…¶жҰӮзҺҮгҖҒж•°еӯҰжңҹжңӣзҡ„и®Ўз®—е…¬ејҸжҳҜи§Јйўҳзҡ„е…ій”®пјҺ |

