+
+…+
，并记f(n)=S2n+1-Sn+1. (1)证明：f(n+1)＞f(n)；
(2)试确定实数m的取值范围，使得对于一切大于1的自然数n，f(n)＞［logm(m-1)］2-
++…+，并记f(n)=S2n+1-Sn+1. (1)证明：f(n+1)＞f(n)；
(2)试确定实数m的取值范围，使得对于一切大于1的自然数n，f(n)＞［logm(m-1)］2-
∵f（n+1）-f（n）=()-()
=＞0，
故f（n+1）＞f（n）.
（2）要使f（n）＞［logm（m-1）］2-
［log（m-1）m］2恒成立，也就是使f（n）min＞［logm（m-1）］2-
［log（m-1）m］2，
因此需先求f（n）min.
由(1)知f（n）单调递增，
故f（n）min=f（2）=
.
于是需解不等式
＞［logm（m-1）］2-
［log（m-1）m］2，
令x=logm（m-1），其中m＞1,且m≠2
＞x2-
·1x2
20x4-9x2-11＜0
（20x2+11）（x2-1）＜0
x2-1＜0
-1＜x＜1
-1＜logm（m-1）＜1
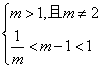
＜m＜2,或m＞2.