和正三角形CDE，AD与BE交与点O，AD与BC交与点P，BE与CD交与点Q，连接PQ

和正三角形CDE，AD与BE交与点O，AD与BC交与点P，BE与CD交与点Q，连接PQ．有下列结论：

①AD=BE；②AP=BQ；③∠AOB=60°；④DE=DP；⑤△CPQ为正三角形．

其中正确的结论有（　　）

A．①②③⑤ B．①③④⑤  C．①②⑤     D．②③④

A【考点】全等三角形的判定与性质；等边三角形的判定与性质．

【分析】根据等边三角形性质得出AC=BC，DC=CE，∠BCA=∠DCE=60°，求出∠ACD=∠BCE，证△ACD≌△BCE，推出AD=BE，即可判断①；根据全等三角形性质得出∠CBE=∠CAD，根据ASA证△ACP≌△BCQ，推出AP=BQ，即可判断②；对应角相等可得∠CAD=∠CBE，然后证明△ACP与△BCQ全等，根据全等三角形对应角相等可得PC=PQ，从而得到△CPQ是等边三角形，所以⑤正确求出∠DCE=60°=∠CAD+∠ADC，求出∠CAD+∠BEC=60°，即可求出∠AOB=60°，即可判断③；根据三角形外角性质推出∠DPC＞∠DCP，推出DP＜DC，即可判断④．

【解答】解：∵△ABC和△DCE是正三角形，

∴AC=BC，DC=CE，∠BCA=∠DCE=60°，

∴∠BCA+∠BCD=∠DCE+∠BCD，

∴∠ACD=∠BCE，

在△ACD和△BCE中

∴△ACD≌△BCE（SAS），

∴AD=BE，∴①正确；

∵△ACD≌△BCE，

∴∠CBE=∠CAD，

∵∠ACB=∠DCE=60°，

∴∠BCD=60°=∠ACB，

在△ACP和△BCQ中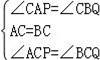

∴△ACP≌△BCQ（ASA），

∴AP=BQ，∴②正确；

PC=QC，

∴△CPQ为正三角形∴⑤正确

∵△ACD≌△BCE，

∴∠ADC=∠BEC，

∠DCE=60°=∠CAD+∠ADC，

∴∠CAD+∠BEC=60°，

∴∠AOB=∠CAD+∠BEC=60°，∴③正确；

∵△DCE是正三角形，

∴DE=DC，

∵∠AOB=60°，∠DCP=60°，∠DPC＞∠AOB，

∴∠DPC＞∠DCP，

∴DP＜DC，即DP＜DE，∴④错误；

所以正确的有①②③⑤，

故选A．