数列{an}满足Sn=2n﹣an(n∈N*).
(Ⅰ)计算a1,a2,a3,a4,并由此猜想通项公式an;
(Ⅱ)用数学归纳法证明(Ⅰ)中的猜想.
数列{an}满足Sn=2n﹣an(n∈N*).
(Ⅰ)计算a1,a2,a3,a4,并由此猜想通项公式an;
(Ⅱ)用数学归纳法证明(Ⅰ)中的猜想.
【考点】RG:数学归纳法;8H:数列递推式;F1:归纳推理.
【分析】(Ⅰ)通过n=1,2,3,4,直接计算a1,a2,a3,a4,并由此猜想通项公式![]()
![]() ;
;
(Ⅱ)直接利用数学归纳法证明.检验n取第一个值时,等式成立,假设![]()
![]() ,证明.
,证明.
【解答】(本小题满分8分)
解:(Ⅰ)当n=1时,a1=s1=2﹣a1,所以a1=1.
当n=2时,a1+a2=s2=2×2﹣a2,所以![]()
![]() .
.
同理:![]()
![]() ,
,![]()
![]() .
.
由此猜想![]()
![]() …
…
(Ⅱ)证明:①当n=1时,左边a1=1,右边=1,结论成立.
②假设n=k(k≥1且k∈N*)时,结论成立,即![]()
![]() ,
,
那么n=k+1时,ak+1=sk+1﹣sk=2(k+1)﹣ak+1﹣2k+ak=2+ak﹣ak+1,
所以2ak+1=2+ak,所以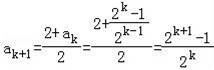
 ,
,
这表明n=k+1时,结论成立.
由①②知对一切n∈N*猜想![]()
![]() 成立.…
成立.…