)=
+
.(1)求函数f(x)的最大值和最小值;
(2)若α、β∈(0,π),f(α)=f(β),且α≠β,求tan(α+β)的值.
)=+.(1)求函数f(x)的最大值和最小值;
(2)若α、β∈(0,π),f(α)=f(β),且α≠β,求tan(α+β)的值.
解:(1)由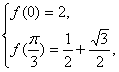得2
解得a=1,b=2,
∴f(x)=sin2x+cos2x+1=2sin(2x+)+1.
∵-1≤sin(2x+
)≤1,
∴f(x)max=
+1,f(x)min=1-
.
(2)由f(α)=f(β),得sin(2α+
)=sin(2β+
).
∵2α+
、2β+
∈(
,
),且α≠β,
∴2α+
=π-(2β+
)或2α+
=3π-(2β+
),
∴α+β=
或α+β=
,
故tan(α+β)=1.