已知幂函数f(x)＝xα的图象经过点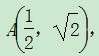
(1)求实数α的值；
(2)用定义证明f(x)在区间(0，＋∞)内的单调性.
已知幂函数f(x)＝xα的图象经过点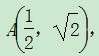
(1)求实数α的值；
(2)用定义证明f(x)在区间(0，＋∞)内的单调性.
解 (1)∵f(x)＝xα的图象经过点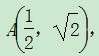
∴
＝
，即2－α＝2
，∴α＝－；
(2)任取x1，x2∈(0，＋∞)，且x1＜x2，则
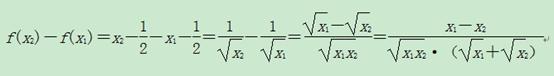∵x2＞x1＞0，∴x1－x2＜0，且
·(
＋
)＞0，于是f(x2)－f(x1)＜0，即f(x2)＜f(x1)，所以f(x)＝x－在区间(0，＋∞)内是减函数.