已知Sn是数列{an}的前n项和,Sn=pn(p∈R,n∈N*),那么数列{an}( )
A.是等比数列 B.当p≠0时是等比数列
C.当p≠0,p≠1时是等比数列 D.不是等比数列
已知Sn是数列{an}的前n项和,Sn=pn(p∈R,n∈N*),那么数列{an}( )
A.是等比数列 B.当p≠0时是等比数列
C.当p≠0,p≠1时是等比数列 D.不是等比数列
D
由Sn=pn(p∈R,n∈N*),得a1=S1=p,并且当n≥2时,an=Sn-Sn-1=pn-pn-1=(p-1)pn-1.
故a2=(p-1)p.
因此数列{an}成等比数列等价于
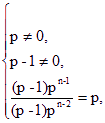
而![]() =
=![]() =p-1.
=p-1.
故满足条件的实数p不存在.