已知a2sin θ＋acos θ－2＝0，b2sin θ＋bcos θ－2＝0(a，b，θ∈R，且a≠b)，直线l过点A(a，a2)，B(b，b2)，则直线l被圆(x－cos θ)2＋(y－sin θ)2＝4所截得的弦长为________．
已知a2sin θ＋acos θ－2＝0，b2sin θ＋bcos θ－2＝0(a，b，θ∈R，且a≠b)，直线l过点A(a，a2)，B(b，b2)，则直线l被圆(x－cos θ)2＋(y－sin θ)2＝4所截得的弦长为________．
2
解题思路：据已知a，b可视为方程x2sin θ＋xcos θ－2＝0的两根，由韦达定理可得a＋b＝－
，ab＝－
，又因为直线AB的方程为y＝(a＋b)x－ab，故圆心到直线距离d＝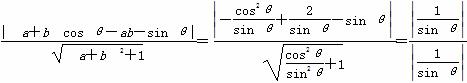
＝1，故所求弦长为2
＝2.